О стали

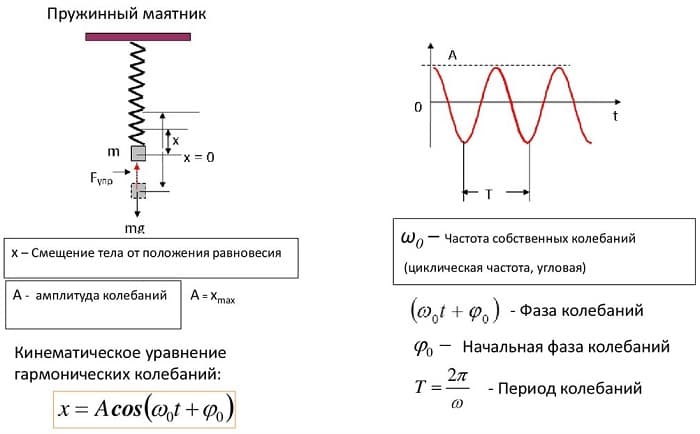
Пружинный маятник — формулы и уравнения нахождения величин. Свободные колебания. Пружинный маятник

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости. 

Приняты следующие обозначения:

• m — масса тела;

• k — коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Виды пружинных маятников

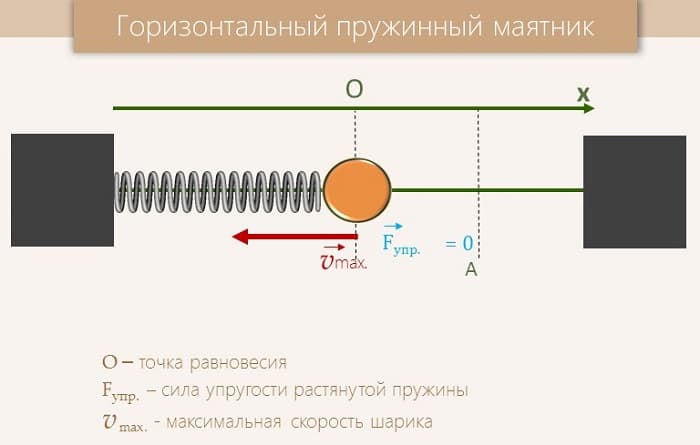
Существует два типа данной системы:

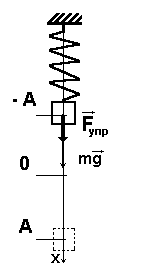
Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.

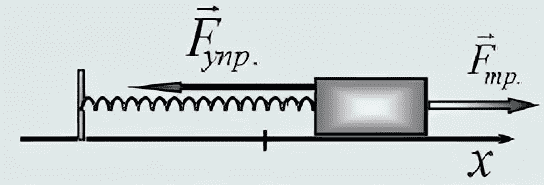
Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением: 

Уравнение гармонических колебаний x = xmaxcos(2πνt) x — координата в момент времени t [м] xmax — амплитуда [м] ν — частота [Гц] t — момент времени [с] π = 3,14

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний φ = 2πνt φ — фаза [рад] ν — частота [Гц] t — момент времени [с] π = 3,14

Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

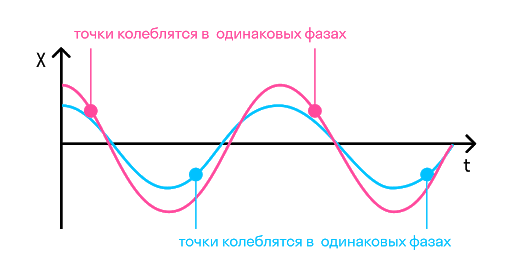
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу. 

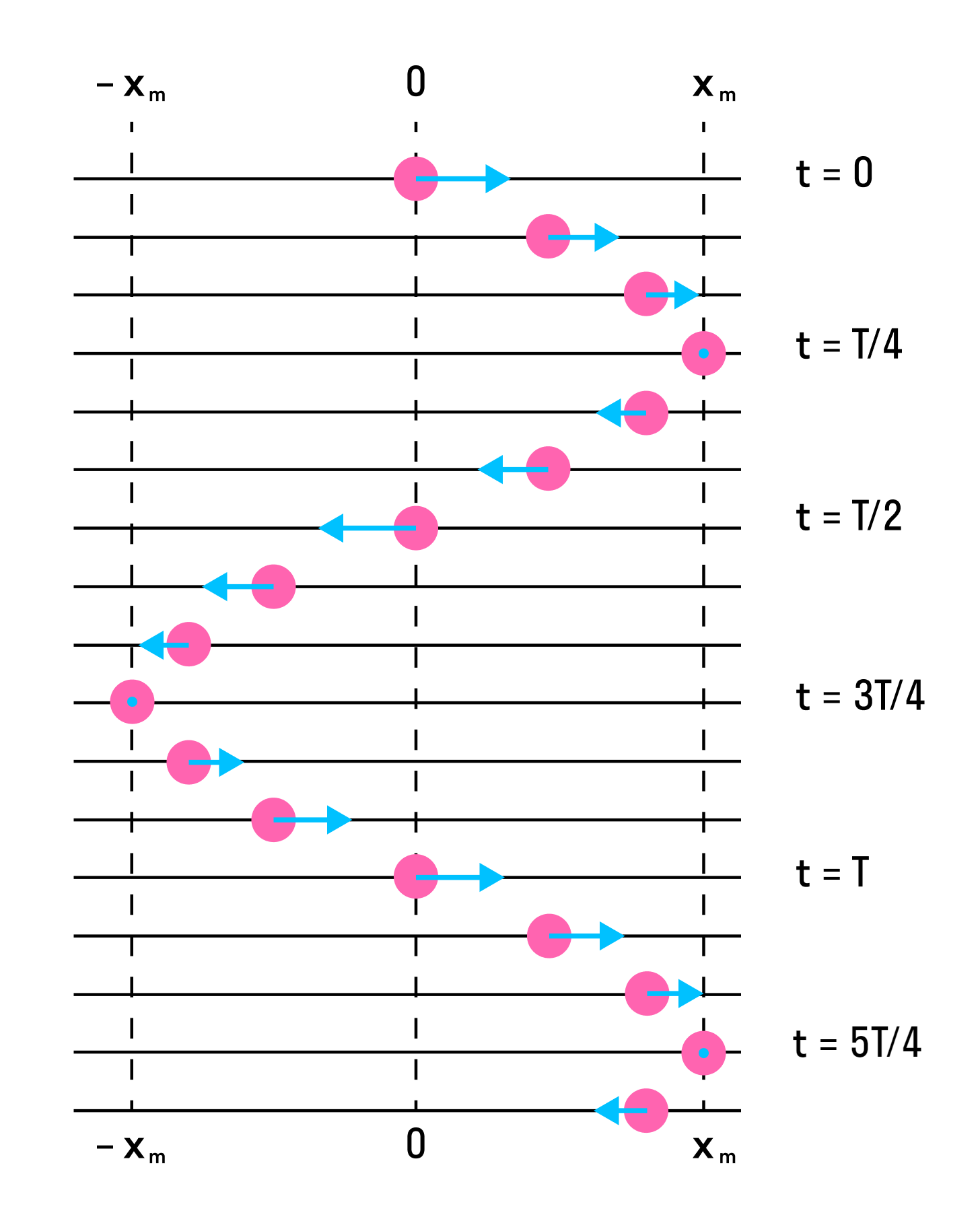
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

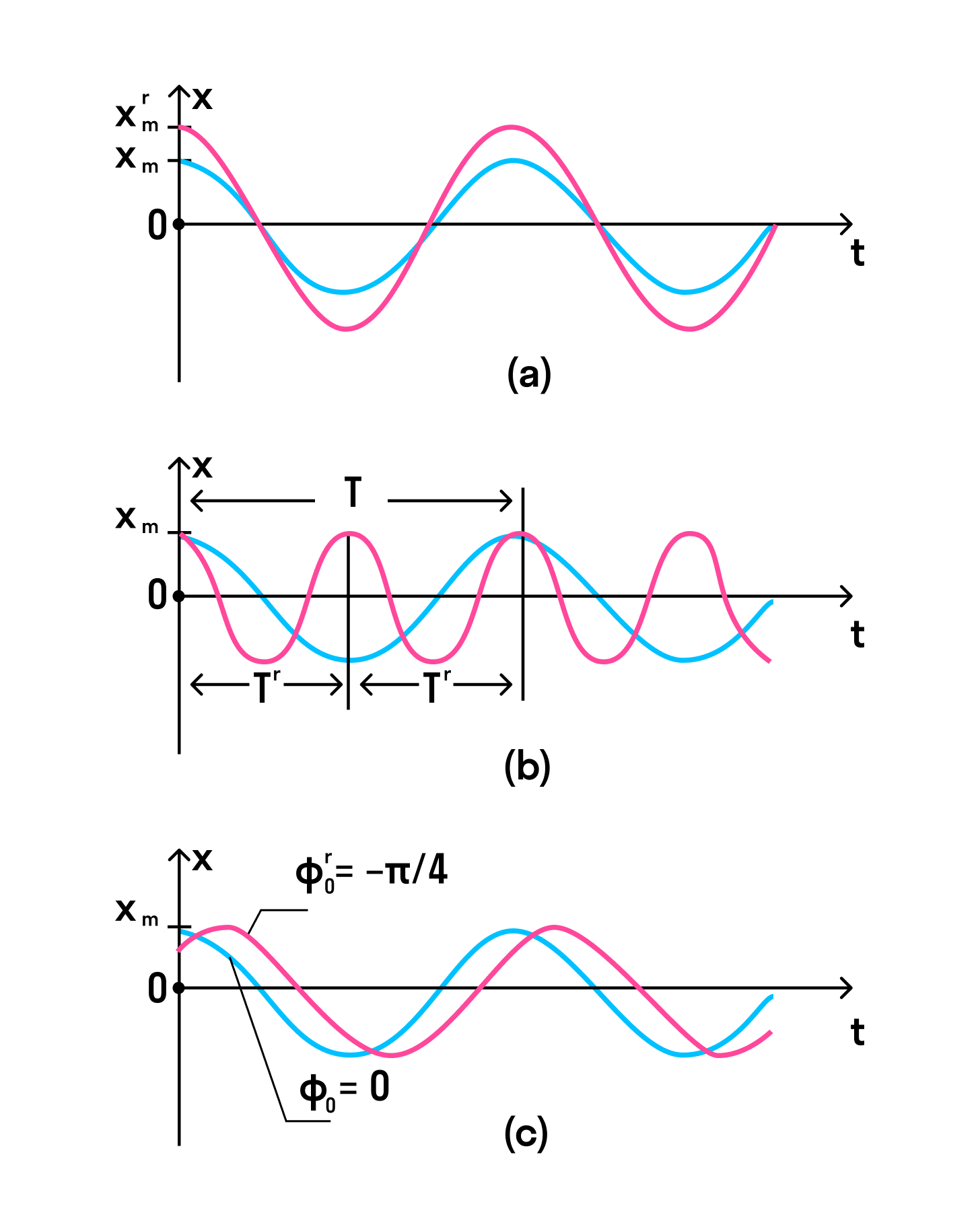
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

• В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

• Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её. 

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

Fупр = — k*x

где k — коэффициент жесткости пружины (Нм),

x – смещение (м).

Дифференциальное уравнение гармонических колебаний пружинного маятника 

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.

Понравилась статья? Поделитесь ей

А какая Ваша оценка этой статьи?

12345
5 из 5

Доска почета

Чтобы сюда попасть — пройдите тест

Что мы узнали?

Круговая (циклическая) частота – это важный параметр гармонического колебания, удобный в математической обработке функций. Круговая частота обозначает количество радиан, прошедших гармонической функцией за единицу времени. Она прямо пропорциональна обычной частоте.

Уравнения колебаний пружинного маятника

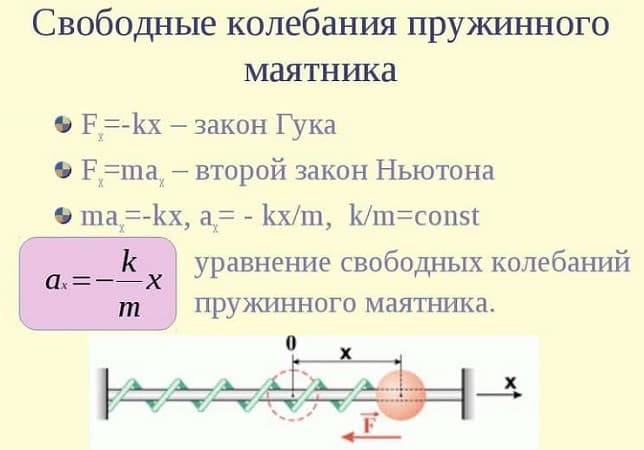
Свободные колебания пружинного маятника описываются с помощью гармонического закона. 

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = — mw2x(t),

где w — радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

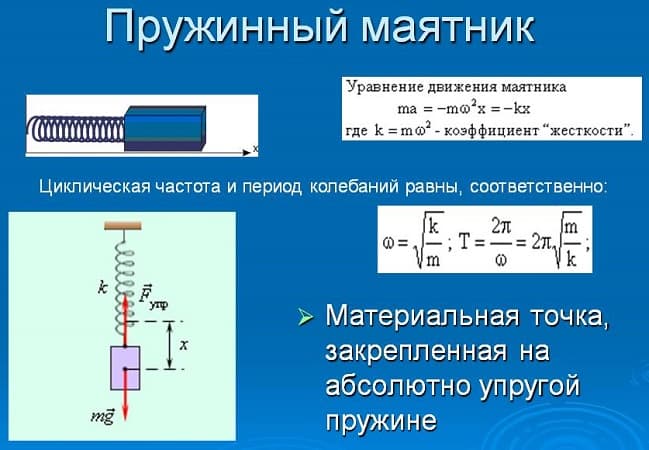
Факторы, от которых зависит частота:

Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии. 

Рассмотрим его на примере математического маятника.

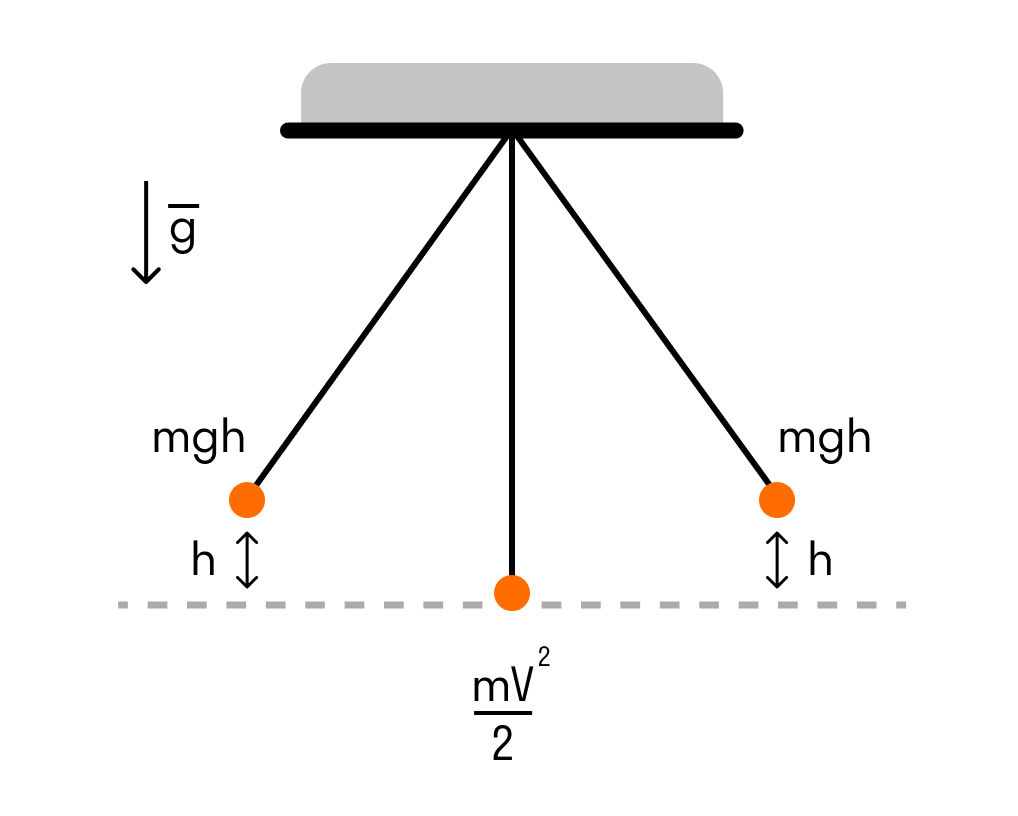
• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

 

• 0
• 0
• 0
• 0
• 0

Выбрать репетитора

Каталог проверенных преподавателей, которые помогут ребёнку влюбиться в предмет и достичь поставленных целей

Все репетиторы Skysmart

Почитать что-то похожее: Поверхностное натяжение Физика

40987

Ускорение свободного падения Физика

67775

Сила тока Физика

17025

Закон электромагнитной индукции Физика

87303

Длина волны Физика

39721

Вынужденные колебания Физика

13548

О школе Процесс обучения Преподаватели Цены Все курсы для детей

Поучиться

Предметы Skysmart

• До школы
• Школьные предметы
• Подготовка к ЕГЭ и ОГЭ
• Программирование
• Кружки
• Заново

Английский язык 4–9 лет
Подготовка к школе 4–7 лет
Английский язык 10–18 лет
Шахматы 4–13 лет
Математика c 1 класса
Обществознание с 7 класса
Русский язык с 2 класса
Физика с 7 класса
Химия с 8 класса
Премиум английский 7–18 лет

Программирование 8–12 лет • Основы
Программирование 12–18 лет • Python
Создание игр 8–18 лет
Создание сайтов 12–18 лет

Школа профессий будущего Групповые уроки Skysmart Класс Английский для взрослых Все курсы для детей

Полезности

Статьи Варианты ВПР Преподавателям Партнёрская программа Отзывы о Skysmart

Соцсети для родителей

Свободные и вынужденные колебания.

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

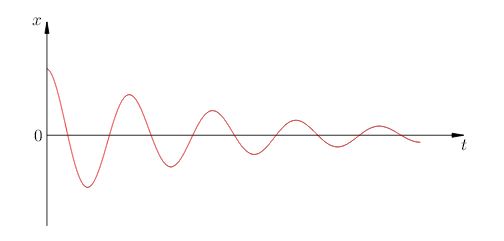Рис. 6. Затухающие колебания

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы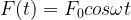
, периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна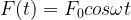
, а вынуждающая сила зависит от времени по гармоническому закону:

.

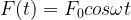
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой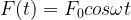

вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

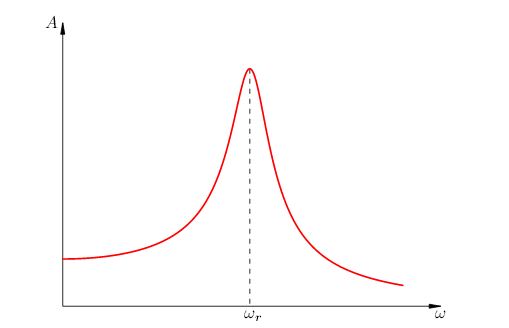Рис. 7. Резонанс

Мы видим, что вблизи частоты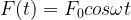
наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: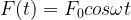
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,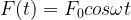
, а амплитуда колебаний возрастает до бесконечности при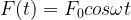
.

Поделиться страницей

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника. 

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Тест по теме

1. /5Вопрос 1 из 5

Формула гармонических колебаний:

• $x=A + t + varphi$
• $x=lg(omega t+varphi)$
• $x=Asin(omega t+varphi)$
• $x=Ae^t$

Начать тест Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Круговая частота

Как видим, физический и математический подход к описанию периода функций несколько отличаются, и возникает вопрос их связи.

Из приведенной выше формулы гармонических колебаний можно видеть, что она имеет период:

$$T = {2pi over omega}$$

В эту формулу входит параметр $omega$, который обратно пропорционален периоду. При сравнении этой формулы с формулой частоты можно получить:

$$T = {2pi over omega}={1over nu}$$

Или, после упрощений:

$$omega = 2pi nu$$

Таким образом, параметр $omega$ в $2pi$ раз больше частоты колебаний. Поскольку в одном круге $2pi$ радиан, то параметр $omega$ называется «круговой» или «циклической» частотой.

Физический смысл частоты – это количество колебаний, происходящих в системе за единицу времени, а физический смысл круговой частоты – это количество радиан, проходящих функцией, описывающей систему, за единицу времени.

Рис. 3. Круговая (циклическая) частота.

Таким образом, удобный и наглядный параметр частоты может быть легко преобразован для вида, удобного в математических преобразованиях.

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Потенциальная энергия:

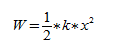
Кинетическая энергия:

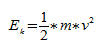
Полная энергия:

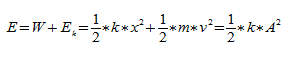
Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

Влияние силы трения при расчете не учитывают.

Характеристики колебаний

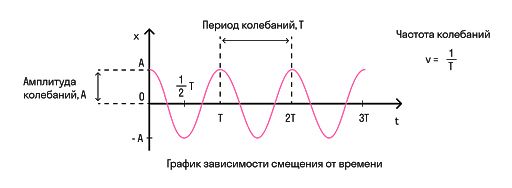
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний T  = t/N T — период [с] t — время [с] N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты ν  = N/t = 1/T ν — частота [Гц] t — время [с] T — период [с] N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.

Она используется в уравнении гармонических колебаний: